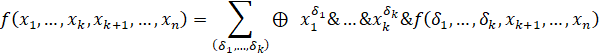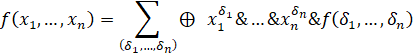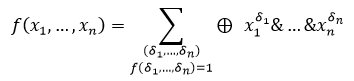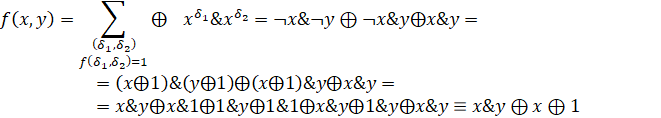The Emissia.Offline Letters           Электронное научное издание (научно-педагогический интернет-журнал)      

Издается с 7 ноября 1995 г.  Учредитель:  Российский государственный педагогический университет им. А.И.Герцена

Смирнова Татьяна Сергеевна
кандидат педагогических наук, доцент, кафедра Информационные системы, Российский государственный педагогический университет им. А. И. Герцена, Санкт-Петербург
Stefanova_t@mail.ru

Обучение построению квантовых оракулов с помощью полиномов Жегалкина

Аннотация
Данная статья описывает подход к отбору содержания обучения построению квантовых оракулов с помощью полиномов Жегалкина, что позволит привести к формированию у обучающихся знаний и умений использования аппарата булевой алгебры для построения простейших квантовых алгоритмов.

Ключевые слова
содержание обучения, средства обучения, квантовый оракул, полином Жегалкина.

_________

Tatyana S. Smirnova
Candidate of Pedagogical Sciences, Associate Professor, Department of Information Systems, A.l. Herzen State Pedagogical University of Russia, St. Petersburg
Stefanova_t@mail.ru

Learning to build quantum oracles using Zhegalkin polynomials

Abstract
This article describes an approach to the selection of training content for building quantum oracles using Zhegalkin polynomials, which will lead to the formation of students' knowledge and skills in using the Boolean algebra apparatus for constructing the simplest quantum algorithms.

Key words
learning content, teaching aids, quantum oracle, Zhegalkin polynomial.

_________

В настоящее время темы, связанные с квантовыми вычислениями, получили широкое распространение, поскольку появились первые квантовые компьютеры. Однако некоторые разделы курса «Квантовые вычисления» все ещё требуют отбора содержания обучения, например, раздел «Построение квантовых оракулов».

Вначале определим необходимые понятия, которые являются основополагающими при изучении данного раздела квантовых вычислений, а именно: понятие «оракул», «квантовый оракул».

Для понимания сущности термина оракул воспользуемся описанием, которое было дано А.Тьюрингом в 1939 году (цит. по [2]): "Давайте представим, что мы обладаем некими неведомыми средствами решения [неразрешимых] теоретико-вычислительных задач, своего рода оракулом... Не вдаваясь в природу этого оракула, скажем только, что он не может быть машиной. С помощью оракула мы могли бы создать новый вид машины (назовём их О-машинами), одной из основных операций которой является решение данной теоретико-числовой задачи".

Естественно, что нам часто хотелось бы иметь в жизни маленького оракула, помогающего в решении по-настоящему трудных вопросов.

Определим понятие оракул с точки зрения теории алгоритмов.

Оракул — это "чёрный ящик", мгновенно выдающий по запросу машины значения функции или умеющий решать за "один шаг" некоторые типы задач.

Тандем машины с оракулом представляет собой новый вычислительный прибор, обладающий иногда более широкими возможностями (по [1]).

Для описания квантового оракула будем опираться на основные понятия булевой алгебры.

Квантовый оракул является способом представления булевой функции , в квантовых вычислениях (непривычная форма записи связана с необходимостью поддержки обратимых вычислений). Другими словами, квантовые оракулы позволяют встраивать классические булевы функции в квантовые схемы.

С другой стороны, понятие квантовый оракул можно определить через квантовые операторы.

Квантовым оракулом называется квантовый оператор , выполняющий унитарное преобразование или
где - n-кубитовое состояние, - однокубитовое состояние.

Другими словами, квантовый оракул представляет собой последовательность квантовых элементов, преобразующая состояние в состояние .

Примерами квантового оракула можно считать квантовые гейты.

;

.

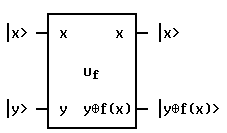
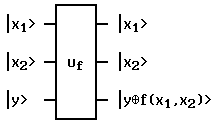
Квантовую схему для квантового оракула часто рассматривают как чёрный ящик и изображают следующим образом:

или

Для построения квантового оракула необходимы знания, связанные с построением полинома Жегалкина для заданной функции и умениями работать с алгебраическими полиномами.

Полиномом Жегалкина называется многочлен, являющийся суммой констант 0 или 1 и различных одночленов, в которые все переменные входят не выше, чем в первой степени:

причём на каждом наборе все различны, .

Теорема (И.И.Жегалкина).

1. Каждая булева функция единственным образом может быть представлена в виде некоторого полинома Жегалкина.
    

2. Система функций полна в классе булевых функций.

Рассмотрим шесть основных методов построения полиномов Жегалкина.

1. Метод неопределённых коэффициентов для построения полинома Жегалкина, реализующего функцию , состоит в следующем.

Рассмотрим полином Жегалкина вида и для каждого составляется уравнение .

Решение полученных уравнений даёт коэффициенты полинома .

Приведем пример построения полинома Жегалкина методом неопределённых коэффициентов для функции .

Ищем выражение для функции в виде полинома с неопределёнными коэффициентами: .

Воспользуемся перебором значений переменных и :

1. ;
    

2. ;
    

3. ;
    

4. .

В результате получаем: .

2. Метод эквивалентных преобразований для построения полинома Жегалкина для функции состоит в следующем:

1. Строим эквивалентный терм над множеством связок ;
    

2. во всей функции терм заменяем на ;
    

3. раскрываем скобки, пользуясь дистрибутивным законом
   
   
   
   и "приводим подобные члены".

Приведем пример построения полинома Жегалкина методом эквивалентных преобразований для функции .

.

3. Метод разложения по переменным.

Для того, чтобы воспользоваться данным методом построения полинома Жегалкина необходима следующая теорема и следствия.

Теорема. Любую булеву функцию   при любом , можно представить в виде:

где суммирование по модулю 2 берётся по всевозможным наборам значений переменных .

Следствие 1 (разложение по всем n переменным).

Следствие 2. Пусть не равна 0 тождественно. Тогда

Это метод удобно использовать для построения полинома Жегалкина функции , если дополнительно воспользоваться тем, что  .

Рассмотрим построение полинома Жегалкина методом разложения по переменным для функции  .

4. Метод треугольника (см. [3]).

Рассмотрим на примере построение полинома Жегалкина методом треугольника для функции  .

Сначала построим строку из значений функции; затем, перемещаясь по этой строке слева направо, выполняем операцию над соседними битами строки. В результате получаем треугольник:

Сложность метода треугольника (по количеству операций & и ) равна .

5. Матричный метод (см. [3]).

Метод предполагает формирование для заданного n матрицы , состоящей из строк и столбцов. Матрица конструируется с помощью следующего рекуррентного соотношения:

.

Коэффициенты полинома Жегалкина определяются с помощью операции умножения по модулю 2 (т.е. операция "+" заменяется на операцию "") матрицы на вектор-столбец из значений, содержащий значения булевой функции. Результатом является столбец из коэффициентов искомого полинома Жегалкина.

Рассмотрим пример построения полинома Жегалкина матричным методом при n=2, :

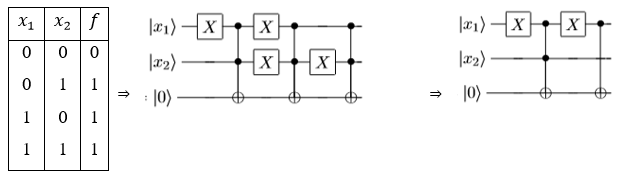
Сложность матричного метода (по количеству операций & и ) равна .

6. Использование системы компьютерной алгебры, на примере, программного пакета Maple для конструирования полинома Жегалкина по заданной пропозициональной формуле.

Продемонстрируем несколько примеров построения квантового оракула.

Пусть дана следующая функция . Построим квантовый оракул.

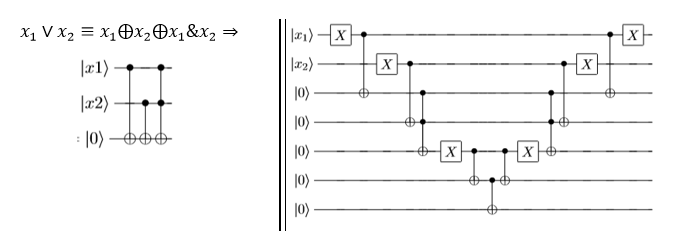
Рассмотрим два способа решения данной задачи.

1. 
   

2. В работе [4] для функции построена квантовая схема, расположенная правее двойной вертикальной черты; мы же воспользовались полиномом Жегалкина для построения квантового оракула:

Второй вариант решения позволяет сделать вывод, что в построенных схемах «выигрышным» вариантом является способ, опирающийся на использование полинома Жегалкина, поскольку во второй схеме количество используемых квантовых проводов и гейтов значительно больше, чем в первой схеме.

Описанные выше базовые понятия позволяют выполнить отбор содержания обучения этому разделу квантовых вычислений.

Выделим следующую последовательность тем.

1. Булевы функции. Основные понятия:

• Булевы векторы, единичный n-мерный куб;
   

• конечные функции, булевы функции (функции алгебры логики), существенные и фиктивные переменные, основные способы задания булевых функций;
   

• основные (элементарные) булевы функции;
   

• термы над множеством;
   

• термы над множеством, суперпозиция, принцип двойственности.

2. Булевы функции. Дизъюнктивные и конъюнктивные нормальные формы, полиномы Жегалкина:

• Разложение булевых функций по переменным, специальные виды термов (дизъюнктивные и конъюнктивные нормальные формы, полином Жегалкина);
   

• методы построения полинома Жегалкина.

3. Квантовые оракулы: схемы и матрицы.

• Квантовый оракул;
   

• конструирование квантовой схемы оракула по заданной булевой функции;
   

• конструирование матрицы оракула по заданной булевой функции;
   

• обобщённые оракулы для булевой функции.

4. Построение квантовых оракулов с помощью полиномов Жегалкина:

• Полином Жегалкина;
   

• положительно поляризованный полином Жегалкина, отрицательно поляризованный полином Жегалкина;
   

• методы построения полинома Жегалкина;
   

• конструирование оракулов с помощью полиномов Жегалкина;
   

• арифметические полиномы.

Данный отбор содержания обучения предполагает выбор средств обучения. Будем считать, что основными средствами обучения являются программный пакет Maple и императивный язык квантового программирования QCL.

В заключение отметим, что:

1. Приведенные способы построения полиномов Жегалкина дают возможность выбора технологии получения квантового оракула.
    

2. Построение квантовых оракулов с использованием полинома Жегалкина является удобным и достаточно иллюстративным методом, который применим в качестве базового для студентов, обучающихся в рамках дисциплины по выбору «Прикладное программирование на языках высокого уровня. Квантовые вычисления».

Литература

1. Босс В. Лекции по математике. Т. 10: Перебор и эффективные алгоритмы: Учебное пособие. — М.: Издательство ЛКИ, 2008. — 216 с.

2. Петцольд Ч. Читаем Тьюринга. Путешествие по исторической статье Тьюринга о вычислимости и машинах Тьюринга. – М.: ДМК Пресс, 2014 г. – 440 с.

3. Супрун В.П. Основы теории булевых функций. - М.: ЛЕНАНД, 2017. - 208 с.

4. Valiron B. Quantum computation: a Tutorial // New Generation Compution, 2012.

Рекомендовано к публикации:
А.А.Ахаян, доктор педагогических наук, член Редакционной Коллегии

Literature

1. Boss V. Lektsii po matematike. T. 10: Perebor i effektivnyye algoritmy: Uchebnoye posobiye. — M.: Izdatel'stvo LKI, 2008. — 216 s.

2. Pettsol'd CH. Chitayem T'yuringa. Puteshestviye po istoricheskoy stat'ye T'yuringa o vychislimosti i mashinakh T'yuringa. – M.: DMK Press, 2014 g. – 440 s.

3. Suprun V.P. Osnovy teorii bulevykh funktsiy. - M.: LENAND, 2017. - 208 s.

4. Valiron B. Quantum computation: a Tutorial // New Generation Compution, 2012.